محتوا

• مراحل

یک معادله مثلثاتی شامل یک یا چند توابع مثلثاتی متغیر "x" (یا هر متغیر دیگر) است. حل معادله مثلثاتی یافتن چنین مقداری "x" است که عملکرد (ها) و معادله را به طور کلی ارضا می کند.

• راه حل معادلات مثلثاتی بر حسب درجه یا رادیان بیان می شود. مثال ها:

x = π / 3 ؛ x = 5π / 6 ؛ x = 3π / 2 ؛ x = 45 درجه ؛ x = 37.12 درجه ؛ x = 178.37 درجه

• توجه: مقادیر توابع مثلثاتی از زاویه ، بیان شده در رادیان و از زاویه ، بیان شده در درجه ، برابر است. یک دایره مثلثاتی با شعاع مساوی یک برای توصیف توابع مثلثاتی و همچنین بررسی صحت حل معادلات و نابرابری های اصلی مثلثاتی استفاده می شود.
• نمونه هایی از معادلات مثلثاتی:
  • sin x + sin 2x = 1/2 ؛ tg x + ctg x = 1.732 ؛
  • cos 3x + sin 2x = cos x؛ 2sin 2x + cos x = 1.

1. یک دایره مثلثاتی با شعاع یک (واحد دایره).
   • این یک دایره با شعاع برابر یک و مرکز آن در نقطه O است. دایره واحد 4 تابع مثلثاتی اساسی متغیر "x" را توصیف می کند ، جایی که "x" زاویه ای است که از جهت مثبت محور X خلاف جهت عقربه های ساعت اندازه گیری می شود.
   • اگر "x" زاویه ای بر روی دایره واحد دارد ، پس:
   • محور افقی OAx تابع F (x) = cos x را تعریف می کند.
   • محور عمودی OBy تابع F (x) = sin x را تعریف می کند.
   • محور عمودی AT تابع F (x) = tan x را تعریف می کند.
   • محور افقی BU تابع F (x) = ctg x را تعریف می کند.

• دایره واحد همچنین برای حل معادلات و نابرابری های اصلی مثلثاتی استفاده می شود (موقعیت های مختلف "x" روی آن در نظر گرفته شده است).

مراحل

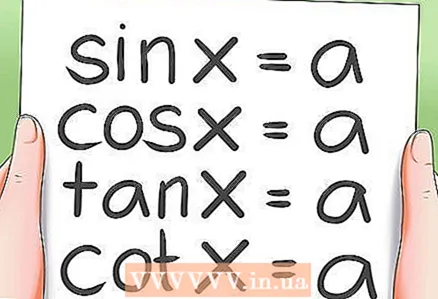1. 1 مفهوم حل معادلات مثلثاتی
   • برای حل معادله مثلثاتی ، آن را به یک یا چند معادله مثلثاتی اساسی تبدیل کنید. حل معادله مثلثاتی در نهایت به حل چهار معادله مثلثاتی اساسی خلاصه می شود.
2. 2 حل معادلات مثلثاتی پایه
   • 4 نوع معادله مثلثاتی اساسی وجود دارد:
   • گناه x = a؛ cos x = a
   • tg x = a ؛ ctg x = a
   • حل معادلات اصلی مثلثاتی شامل نگاه کردن به موقعیت های مختلف x در دایره واحد و استفاده از یک جدول تبدیل (یا ماشین حساب) است.
   • مثال 1. گناه x = 0.866. با استفاده از یک جدول تبدیل (یا ماشین حساب) ، پاسخ را دریافت می کنید: x = π / 3. دایره واحد پاسخ دیگری می دهد: 2π / 3. به یاد داشته باشید: همه توابع مثلثاتی دوره ای هستند ، یعنی مقادیر آنها تکرار می شود. به عنوان مثال ، دوره ای بودن گناه x و cos x 2πn است و دوره تناوبی tg x و ctg x πn. بنابراین ، پاسخ به شرح زیر نوشته می شود:
   • x1 = π / 3 + 2πn؛ x2 = 2π / 3 + 2πn.
   • مثال 2.cos x = -1/2. با استفاده از یک جدول تبدیل (یا ماشین حساب) ، پاسخ را دریافت می کنید: x = 2π / 3. دایره واحد پاسخ دیگری می دهد: -2π / 3.
   • x1 = 2π / 3 + 2π؛ x2 = -2π / 3 + 2π.
   • مثال 3.tg (x - π / 4) = 0.
   • پاسخ: x = π / 4 + πn.
   • مثال 4. ctg 2x = 1.732.
   • پاسخ: x = π / 12 + πn.
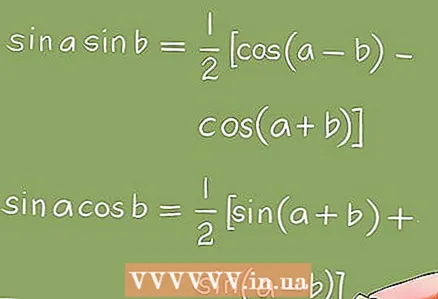3. 3 تحولات مورد استفاده برای حل معادلات مثلثاتی
   • برای تبدیل معادلات مثلثاتی ، از تغییرات جبری (فاکتورگیری ، کاهش اصطلاحات همگن و غیره) و هویت های مثلثاتی استفاده می شود.
   • مثال 5. با استفاده از هویت های مثلثاتی ، معادله sin x + sin 2x + sin 3x = 0 به معادله 4cos x * sin (3x / 2) * cos (x / 2) = 0 تبدیل می شود. بنابراین ، شما باید معادلات مثلثاتی زیر را حل کنید: cos x = 0؛ گناه (3x / 2) = 0 ؛ cos (x / 2) = 0.
     
     
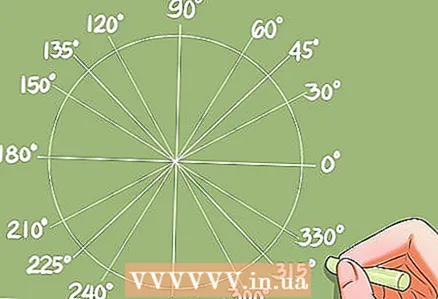4. 4 یافتن زاویه از مقادیر شناخته شده توابع.
   • قبل از یادگیری روشهای حل معادلات مثلثاتی ، باید نحوه پیدا کردن زاویه از مقادیر شناخته شده توابع را بیاموزید. این را می توان با استفاده از یک جدول تبدیل یا ماشین حساب انجام داد.
   • مثال: cos x = 0.732. ماشین حساب جواب x = 42.95 درجه را می دهد. دایره واحد زوایای اضافی خواهد داد که کسینوس آن نیز 0.732 است.
5. 5 محلول را روی دایره واحد کنار بگذارید.
   • می توانید راه حل های معادله مثلثاتی را بر روی دایره واحد موکول کنید. راه حل های معادله مثلثاتی بر روی دایره واحد راس یک چند ضلعی منظم است.
   • مثال: راه حل های x = π / 3 + πn / 2 در واحد واحد راس یک مربع است.
   • مثال: محلول های x = π / 4 + πn / 3 در واحد واحد نشان دهنده راس های یک شش ضلعی معمولی است.
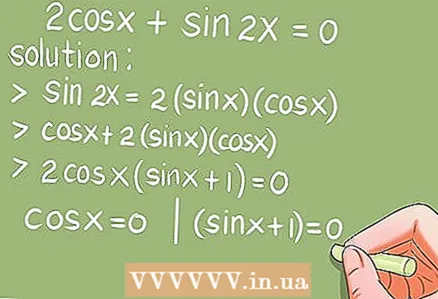6. 6 روشهای حل معادلات مثلثاتی
   • اگر معادله تریگ داده شده فقط شامل یک تابع تریگ باشد ، آن معادله را به عنوان معادله تریگ اساسی حل کنید.اگر یک معادله معین شامل دو یا چند تابع مثلثاتی باشد ، 2 روش برای حل چنین معادله ای وجود دارد (بسته به احتمال تبدیل آن).
     • روش 1
   • این معادله را به معادله ای از شکل تبدیل کنید: f (x) * g (x) * h (x) = 0 ، جایی که f (x) ، g (x) ، h (x) معادلات اصلی مثلثاتی هستند.
     
     
   • مثال 6.2cos x + sin 2x = 0. (0 x 2π)
   • راه حل. با استفاده از فرمول دو زاویه sin 2x = 2 * sin x * cos x ، sin 2x را جایگزین کنید.
   • 2cos x + 2 * sin x * cos x = 2cos x * (sin x + 1) = 0. حالا دو معادله مثلثاتی اساسی را حل کنید: cos x = 0 و (sin x + 1) = 0.
   • مثال 7.cos x + cos 2x + cos 3x = 0. (0 x 2π)
   • راه حل: با استفاده از هویت های مثلثاتی ، این معادله را به معادله ای از شکل تبدیل کنید: cos 2x (2cos x + 1) = 0. حالا دو معادله مثلثاتی اساسی را حل کنید: cos 2x = 0 و (2cos x + 1) = 0.
   • مثال 8.sin x - sin 3x = cos 2x. (0 x 2π)
   • راه حل: با استفاده از هویت های مثلثاتی ، این معادله را به معادله ای از شکل تبدیل کنید: -cos 2x * (2sin x + 1) = 0. حالا دو معادله مثلثاتی اساسی را حل کنید: cos 2x = 0 و (2sin x + 1) = 0
     • روش 2
   • معادله مثلثاتی داده شده را به معادله ای که فقط یک تابع مثلثاتی دارد ، تبدیل کنید. سپس این تابع مثلثاتی را با مواردی ناشناخته جایگزین کنید ، برای مثال t (sin x = t ؛ cos x = t ؛ cos 2x = t ، tg x = t ؛ tg (x / 2) = t و غیره).
   • مثال 9.3sin ^ 2 x - 2cos ^ 2 x = 4sin x + 7 (0 x 2π).
   • راه حل. در این معادله (cos ^ 2 x) را با (1 - sin ^ 2 x) (بر اساس هویت) جایگزین کنید. معادله تبدیل شده عبارت است از:
   • 3sin ^ 2 x - 2 + 2sin ^ 2 x - 4sin x - 7 = 0. sin x را با t جایگزین کنید. این معادله اکنون به این شکل است: 5t ^ 2 - 4t - 9 = 0. این یک معادله درجه دو با دو ریشه است: t1 = -1 و t2 = 9/5. ریشه دوم t2 محدوده مقادیر تابع (-1 sin x 1) را برآورده نمی کند. حالا تصمیم بگیرید: t = sin x = -1؛ x = 3π / 2.
   • مثال 10.tg x + 2 tg ^ 2 x = ctg x + 2
   • راه حل. tg x را با t جایگزین کنید. معادله اصلی را به صورت زیر بازنویسی کنید: (2t + 1) (t ^ 2 - 1) = 0. حالا t را پیدا کرده و سپس x را برای t = tg x پیدا کنید.
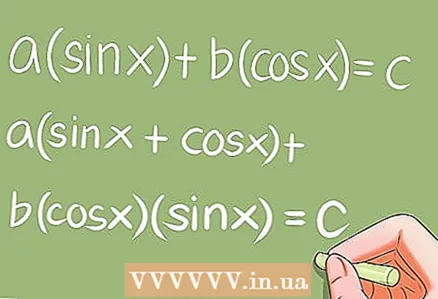7. 7 معادلات مثلثاتی ویژه
   • چندین معادله مثلثاتی خاص وجود دارد که نیاز به تغییراتی خاص دارند. مثال ها:
   • a * sin x + b * cos x = c؛ a (sin x + cos x) + b * cos x * sin x = c؛
   • a * sin ^ 2 x + b * sin x * cos x + c * cos ^ 2 x = 0
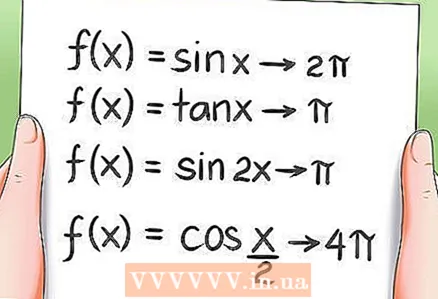8. 8 دوره ای بودن توابع مثلثاتی.
   • همانطور که قبلاً ذکر شد ، همه توابع مثلثاتی دوره ای هستند ، یعنی مقادیر آنها پس از یک دوره خاص تکرار می شود. مثال ها:
     • دوره تابع f (x) = sin x 2π است.
     • دوره تابع f (x) = tan x برابر π است.
     • دوره تابع f (x) = sin 2x π است.
     • دوره تابع f (x) = cos (x / 2) 4π است.
   • اگر دوره در مسئله مشخص شده است ، مقدار "x" را در این مدت محاسبه کنید.
   • توجه: حل معادلات مثلثاتی کار آسانی نیست و اغلب منجر به خطا می شود. بنابراین پاسخ های خود را با دقت بررسی کنید. برای انجام این کار ، می توانید از یک ماشین حساب نمودار برای رسم معادله داده شده R (x) = 0 استفاده کنید. در چنین مواردی ، راه حل ها به صورت کسر اعشاری ارائه می شوند (یعنی π با 3.14 جایگزین می شود).