محتوا

• مراحل
• روش 1 از 3: چگونه معادله مکعبی را بدون یک عبارت ثابت حل کنیم
• روش 2 از 3: چگونه می توان ریشه های کامل را با استفاده از ضرب کننده ها پیدا کرد
• روش 3 از 3: چگونه می توان معادله را با استفاده از تبعیض کننده حل کرد

در یک معادله مکعبی ، بیشترین نمره 3 است ، چنین معادله ای دارای 3 ریشه (راه حل) است و شکل آن ${ displaystyle ax ^ {3} + bx ^ {2} + cx + d = 0}$... حل برخی از معادلات مکعبی چندان آسان نیست ، اما اگر از روش صحیح (با زمینه نظری خوب) استفاده کنید ، می توانید ریشه های پیچیده ترین معادله مکعب را نیز بیابید - برای این منظور از فرمول حل معادله درجه دوم استفاده کنید. ریشه های کامل ، و یا محاسبه تمایز.

مراحل

روش 1 از 3: چگونه معادله مکعبی را بدون یک عبارت ثابت حل کنیم

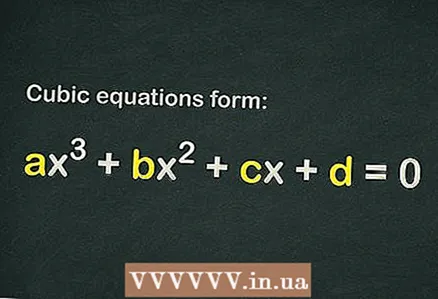1. 1 ببینید آیا در معادله مکعب یک عبارت آزاد وجود دارد یا خیر د{ displaystyle d}. معادله مکعب شکل دارد ${ displaystyle ax ^ {3} + bx ^ {2} + cx + d = 0}$... برای این که یک معادله مکعبی در نظر گرفته شود ، کافی است فقط یک عبارت را در نظر بگیرید ${ displaystyle x ^ {3}}$ (یعنی ممکن است اصلاً هیچ عضو دیگری وجود نداشته باشد).
   • اگر معادله دارای یک عبارت آزاد باشد ${ displaystyle d}$، از روش متفاوتی استفاده کنید.
   • اگر در معادله ${ displaystyle a = 0}$، مکعبی نیست
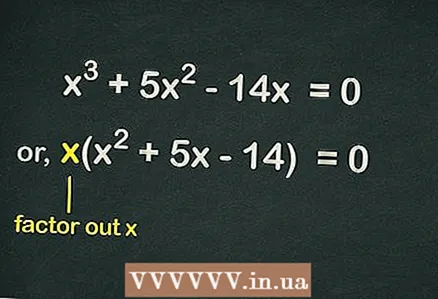2. 2 از براکت ها بیرون بیاورید ایکس{ displaystyle x}. از آنجا که هیچ عبارت آزاد در معادله وجود ندارد ، هر عبارت در معادله شامل متغیر است ${ displaystyle x}$... این بدان معناست که یکی ${ displaystyle x}$ برای ساده تر کردن معادله می توان از پرانتز حذف کرد. بنابراین ، معادله به این صورت نوشته می شود: ${ displaystyle x (ax ^ {2} + bx + c)}$.
   • به عنوان مثال ، با استفاده از یک معادله مکعبی ${ displaystyle 3x ^ {3} -2x ^ {2} + 14x = 0}$
   • بیرون بردن ${ displaystyle x}$ براکت و دریافت کنید ${ displaystyle x (3x ^ {2} -2x + 14) = 0}$
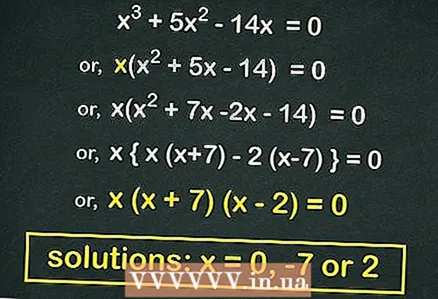3. 3 ضریب (حاصل دو جمله ای) معادله درجه دوم (در صورت امکان). بسیاری از معادلات درجه دوم فرم ${ displaystyle ax ^ {2} + bx + c = 0}$ را می توان فاکتور گرفت اگر معادله را برداریم چنین معادله ای شکل می گیرد ${ displaystyle x}$ خارج از براکت در مثال ما:
   • از براکت ها بیرون بیاورید ${ displaystyle x}$: ${ displaystyle x (x ^ {2} + 5x-14) = 0}$
   • معادله درجه دوم را محاسبه کنید: ${ displaystyle x (x + 7) (x-2) = 0}$
   • هر سطل زباله را برابر کنید ${ displaystyle 0}$... ریشه های این معادله عبارتند از: ${ displaystyle x = 0 ، x = -7 ، x = 2}$.
4. 4 معادله درجه دوم را با استفاده از فرمول مخصوص حل کنید. اگر معادله درجه دوم را نمی توان فاکتور گرفت ، این کار را انجام دهید. برای یافتن دو ریشه یک معادله ، مقادیر ضرایب ${ displaystyle a}$, ${ displaystyle b}$, ${ displaystyle c}$ جایگزین در فرمول ${ displaystyle { frac {-b pm { sqrt {b ^ {2} -4ac}}} {2a}}}$.
   • در مثال ما ، مقادیر ضرایب را جایگزین کنید ${ displaystyle a}$, ${ displaystyle b}$, ${ displaystyle c}$ (${ displaystyle 3}$, ${ displaystyle -2}$, ${ displaystyle 14}$) به فرمول:

     ${ displaystyle { frac {-b pm { sqrt {b ^ {2} -4ac}}} {2a}}}$

     ${ displaystyle { frac {- (- 2) pm { sqrt {((-2) ^ {2} -4 (3) (14)}}} {2 (3)}}}$

     ${ displaystyle { frac {2 pm { sqrt {4- (12) (14)}}} {6}}}$

     ${ displaystyle { frac {2 pm { sqrt {(4-168}}} {6}}}$

     ${ displaystyle { frac {2 pm { sqrt {-164}}} {6}}}$

   • ریشه اول:

     ${ displaystyle { frac {2 + { sqrt {-164}}} {6}}}$

     ${ displaystyle { frac {2 + 12،8i} {6}}}$

   • ریشه دوم:

     ${ displaystyle { frac {2-12،8i} {6}}}$

5. 5 برای حل معادله مکعب از ریشه های صفر و درجه دوم استفاده کنید. معادلات درجه دوم دو ریشه دارند ، در حالی که معادلات مکعبی سه ریشه دارند. شما قبلاً دو راه حل پیدا کرده اید - اینها ریشه معادله درجه دوم هستند. اگر "x" را خارج از پرانتز قرار دهید ، راه حل سوم این خواهد بود ${ displaystyle 0}$.
   • اگر "x" را از براکت بیرون بیاورید ، بدست می آورید ${ displaystyle x (ax ^ {2} + bx + c) = 0}$، یعنی دو عامل: ${ displaystyle x}$ و یک معادله درجه دوم در پرانتز. اگر هریک از این عوامل باشد ${ displaystyle 0}$، کل معادله نیز برابر است ${ displaystyle 0}$.
   • بنابراین ، دو ریشه یک معادله درجه دوم ، راه حل های یک معادله مکعبی هستند. راه حل سوم این است ${ displaystyle x = 0}$.

روش 2 از 3: چگونه می توان ریشه های کامل را با استفاده از ضرب کننده ها پیدا کرد

1. 1 مطمئن شوید که یک عبارت آزاد در معادله مکعب وجود دارد د{ displaystyle d}. اگر در یک معادله از شکل ${ displaystyle ax ^ {3} + bx ^ {2} + cx + d = 0}$ یک عضو رایگان وجود دارد ${ displaystyle d}$ (که برابر با صفر نیست) ، قرار دادن "x" در خارج از پرانتز کار نخواهد کرد. در این مورد ، از روشی که در این قسمت ذکر شده است استفاده کنید.
   • به عنوان مثال ، با استفاده از یک معادله مکعبی ${ displaystyle 2x ^ {3} + 9x ^ {2} + 13x = -6}$... برای بدست آوردن صفر در سمت راست معادله ، اضافه کنید ${ displaystyle 6}$ به دو طرف معادله
   • معادله شکل می گیرد ${ displaystyle 2x ^ {3} + 9x ^ {2} + 13x + 6 = 0}$... مانند ${ displaystyle d = 6}$، از روش توصیف شده در قسمت اول نمی توان استفاده کرد.
2. 2 عوامل ضریب را بنویسید آ{ displaystyle a} و یک عضو رایگان د{ displaystyle d}. یعنی عوامل عدد at را بیابید ${ displaystyle x ^ {3}}$ و اعداد قبل از علامت برابر. به یاد بیاورید که عوامل یک عدد اعدادی هستند که در صورت ضرب ، آن عدد را تولید می کنند.
   • به عنوان مثال ، برای بدست آوردن شماره 6، شما باید ضرب کنید ${ displaystyle 6 بار 1}$ و ${ displaystyle 2 بار 3}$... بنابراین اعداد 1, 2, 3, 6 عوامل تعداد هستند 6.
   • در معادله ما ${ displaystyle a = 2}$ و ${ displaystyle d = 6}$... ضرب کننده ها 2 هستند 1 و 2... ضرب کننده ها 6 اعداد هستند 1, 2, 3 و 6.
3. 3 هر عامل را تقسیم کنید آ{ displaystyle a} برای هر عامل د{ displaystyle d}. در نتیجه ، تعداد زیادی کسر و چندین عدد صحیح بدست می آورید. ریشه های معادله مکعب یکی از اعداد صحیح یا مقدار منفی یکی از اعداد صحیح خواهد بود.
   • در مثال ما ، عوامل را تقسیم کنید ${ displaystyle a}$ (1 و 2) بر اساس عوامل ${ displaystyle d}$ (1, 2, 3 و 6) شما دریافت می کنید: ${ displaystyle 1}$, ${ displaystyle { frac {1} {2}}}$, ${ displaystyle { frac {1} {3}}}$, ${ displaystyle { frac {1} {6}}}$, ${ displaystyle 2}$ و ${ displaystyle { frac {2} {3}}}$... حال مقادیر منفی کسرها و اعداد بدست آمده را به این لیست اضافه کنید: ${ displaystyle 1}$, ${ displaystyle -1}$, ${ displaystyle { frac {1} {2}}}$, ${ displaystyle - { frac {1} {2}}}$, ${ displaystyle { frac {1} {3}}}$, ${ displaystyle - { frac {1} {3}}}$, ${ displaystyle { frac {1} {6}}}$, ${ displaystyle - { frac {1} {6}}}$, ${ displaystyle 2}$, ${ displaystyle -2}$, ${ displaystyle { frac {2} {3}}}$ و ${ displaystyle - { frac {2} {3}}}$... کل ریشه های معادله مکعب برخی از اعداد موجود در این لیست است.
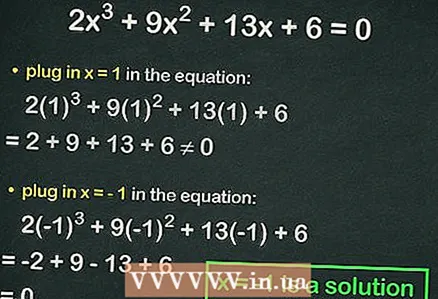4. 4 اعداد صحیح را به معادله مکعب وصل کنید. اگر برابری درست باشد ، عدد جایگزین ریشه معادله است. به عنوان مثال ، در معادله جایگزین کنید ${ displaystyle 1}$:
   • ${ displaystyle 2 (1) ^ {3} +9 (1) ^ {2} +13 (1) +6}$ = ${ displaystyle 2 + 9 + 13 + 6}$ 0 پوند ، یعنی برابری رعایت نمی شود. در این حالت ، شماره بعدی را وصل کنید.
   • جایگزین ${ displaystyle -1}$: ${ displaystyle (-2) +9 +(- 13) +6}$ = 0. بنابراین ، ${ displaystyle -1}$ کل ریشه معادله است.
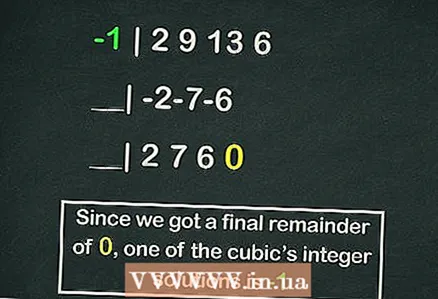5. 5 از روش تقسیم چند جمله ای بر طرح هورنرریشه های معادله را سریعتر بیابید. اگر نمی خواهید اعداد را به صورت دستی در معادله جایگزین کنید ، این کار را انجام دهید. در طرح هورنر ، اعداد صحیح با مقادیر ضرایب معادله تقسیم می شوند ${ displaystyle a}$, ${ displaystyle b}$, ${ displaystyle c}$ و ${ displaystyle d}$... اگر اعداد به طور مساوی تقسیم پذیر باشند (یعنی بقیه اینطور است ${ displaystyle 0}$) ، یک عدد صحیح ریشه معادله است.
   • طرح هورنر مستحق یک مقاله جداگانه است ، اما مثال زیر محاسبه یکی از ریشه های معادله مکعبی ما با استفاده از این طرح است:

     -1 | 2 9 13 6

     __| -2-7-6

     __| 2 7 6 0

   • بنابراین باقی مانده است ${ displaystyle 0}$، ولی ${ displaystyle -1}$ یکی از ریشه های معادله است.

روش 3 از 3: چگونه می توان معادله را با استفاده از تبعیض کننده حل کرد

1. 1 مقادیر ضرایب معادله را بنویسید آ{ displaystyle a}, ب{ displaystyle b}, ج{ displaystyle c} و د{ displaystyle d}. توصیه می کنیم مقادیر ضرایب نشان داده شده را از قبل بنویسید تا در آینده دچار سردرگمی نشوید.
   • به عنوان مثال ، با توجه به معادله ${ displaystyle x ^ {3} -3x ^ {2} + 3x -1}$... بنویس ${ displaystyle a = 1}$, ${ displaystyle b = -3}$, ${ displaystyle c = 3}$ و ${ displaystyle d = -1}$... به یاد بیاورید که اگر قبلا ${ displaystyle x}$ هیچ عددی وجود ندارد ، ضریب مربوطه هنوز وجود دارد و برابر است ${ displaystyle 1}$.
2. 2 تفکیک صفر را با استفاده از فرمول ویژه محاسبه کنید. برای حل معادله مکعبی با استفاده از ممیز ، باید تعدادی محاسبات دشوار انجام دهید ، اما اگر تمام مراحل را به درستی انجام دهید ، این روش برای حل پیچیده ترین معادلات مکعبی ضروری خواهد بود. اولین محاسبه ${ displaystyle Delta _ {0}}$ (صفر متمایز) اولین مقداری است که ما به آن نیاز داریم. برای انجام این کار ، مقادیر مربوطه را در فرمول جایگزین کنید ${ displaystyle Delta _ {0} = b ^ {2} -3ac}$.
   • متمایز کننده عددی است که ریشه های چند جمله ای را مشخص می کند (برای مثال ، متمایز کننده معادله درجه دوم با فرمول محاسبه می شود. ${ displaystyle b ^ {2} -4ac}$).
   • در معادله ما:

     ${ displaystyle b ^ {2} -3ac}$

     ${ displaystyle (-3) ^ {2} -3 (1) (3)}$

     ${ displaystyle 9-3 (1) (3)}$

     ${ displaystyle 9-9 = 0 = دلتا _ {0}}$

3. 3 اولین متمایز کننده را با استفاده از فرمول محاسبه کنید Δ1=2ب3−9آبج+27آ2د{ displaystyle Delta _ {1} = 2b ^ {3} -9abc + 27a ^ {2} d}. اول تبعیض آمیز ${ displaystyle Delta _ {1}}$ - این دومین مقدار مهم است ؛ برای محاسبه آن ، مقادیر مربوطه را به فرمول مشخص شده وصل کنید.
   • در معادله ما:

     ${ displaystyle 2 (-3) ^ {3} -9 (1) (- 3) (3) +27 (1) ^ {2} (- 1)}$

     ${ displaystyle 2 (-27) -9 (-9) +27 (-1)}$

     ${ displaystyle -54 + 81-27}$

     ${ displaystyle 81-81 = 0 = دلتا _ {1}}$

4. 4 محاسبه:${ displaystyle Delta = ( Delta _ {1} ^ {2} -4 Delta _ {0} ^ {3}) div -27a ^ {2}}$... یعنی از طریق مقادیر بدست آمده ، معادله مکعبی را پیدا کنید ${ displaystyle Delta _ {0}}$ و ${ displaystyle Delta _ {1}}$... اگر متمایز یک معادله مکعب مثبت باشد ، این معادله دارای سه ریشه است. اگر ممیز صفر باشد ، معادله یک یا دو ریشه دارد. اگر ممیز منفی باشد ، معادله یک ریشه دارد.
   • یک معادله مکعبی همیشه حداقل یک ریشه دارد ، زیرا نمودار این معادله حداقل در یک نقطه محور X را قطع می کند.
   • در معادله ما ${ displaystyle Delta _ {0}}$ و ${ displaystyle Delta _ {1}}$ برابر هستند ${ displaystyle 0}$، بنابراین می توانید به راحتی محاسبه کنید ${ displaystyle Delta}$:

     ${ displaystyle ( Delta _ {1} ^ {2} -4 Delta _ {0} ^ {3}) div (-27a ^ {2})}$

     ${ displaystyle ((0) ^ {2} -4 (0) ^ {3}) div (-27 (1) ^ {2})}$

     ${ displaystyle 0-0 div 27}$

     ${ displaystyle 0 = دلتا}$... بنابراین ، معادله ما یک یا دو ریشه دارد.

5. 5 محاسبه:${ displaystyle C = ^ {3} { sqrt { left ({ sqrt { Delta _ {1} ^ {2} -4 Delta _ {0} ^ {3}}} + Delta _ {1 } right) div 2}}}$. ${ displaystyle C}$ - این آخرین مقدار مهمی است که یافت می شود. این به شما کمک می کند تا ریشه های معادله را محاسبه کنید. مقادیر را در فرمول مشخص شده جایگزین کنید ${ displaystyle Delta _ {1}}$ و ${ displaystyle Delta _ {0}}$.
   • در معادله ما:

     ${ displaystyle ^ {3} { sqrt {{ sqrt {( Delta _ {1} ^ {2} -4 Delta _ {0} ^ {3}) + Delta _ {1}}} div 2}}}$

     ${ displaystyle ^ {3} { sqrt {{ sqrt {(0 ^ {2} -4 (0) ^ {3}) + (0)}} div 2}}}$

     ${ displaystyle ^ {3} { sqrt {{ sqrt {(0-0) +0}} div 2}}}$

     ${ displaystyle 0 = C}$

6. 6 سه ریشه معادله را بیابید. این کار را با فرمول انجام دهید ${ displaystyle - (b + u ^ {n} C + Delta _ {0} div (u ^ {n} C)) div 3a}$، جایی که ${ displaystyle u = (- 1 + { sqrt {-3}}) div 2}$، ولی n برابر است با 1, 2 یا 3... مقادیر مناسب را در این فرمول جایگزین کنید - در نتیجه ، سه ریشه از معادله را دریافت خواهید کرد.
   • مقدار را با استفاده از فرمول در محاسبه کنید n = 1, 2 یا 3و سپس پاسخ را بررسی کنید. اگر هنگام بررسی پاسخ خود 0 دریافت کنید ، این مقدار ریشه معادله است.
   • در مثال ما ، جایگزین 1 که در ${ displaystyle x ^ {3} -3x ^ {2} + 3x -1}$ و بدست آوردن 0، یعنی 1 یکی از ریشه های معادله است.